Robot localization using a particle system monad
Refactoring Probability Distributions: part 1, part 2, part 3, part 4, part 5
Welcome to the 5th (and final) installment of Refactoring Probability Distributions! Today, let’s begin with an example from Bayesian Filters for Location Estimation (PDF), an excellent paper by Fox and colleagues.
In their example, we have a robot in a hallway with 3 doors. Unfortunately, we don’t know where in the hallway the robot is located:

The vertical black lines are “particles.” Each particle represents a possible location of our robot, chosen at random along the hallway. At first, our particles are spread along the entire hallway (the top row of black lines). Each particle begins life with a weight of 100%, represented by the height of the black line.
Now imagine that our robot has a “door sensor,” which currently tells us that we’re in front of a door. This allows us to rule out any particle which is located between doors.
So we multiply the weight of each particle by 100% (if it’s in front of a door) or 0% (if it’s between doors), which gives us the lower row of particles. If our sensor was less accurate, we might use 90% and 10%, respectively.
What would this example look like in Haskell? We could build a giant list of particles (with weights), but that would require us to do a lot of bookkeeping by hand. Instead, we use a monad to hide all the details, allowing us to work with a single particle at a time.
localizeRobot :: WPS Int
localizeRobot = do
-- Pick a random starting location.
-- This will be our first particle.
pos1 <- uniform [0..299]
-- We know we're at a door. Particles
-- in front of a door get a weight of
-- 100%, others get 0%.
if doorAtPosition pos1
then weight 1
else weight 0
-- ...
What happens if our robot drives forward?
Driving down the hall
When our robot drives forward, we need to move our particles the same amount:
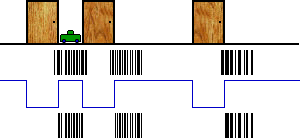
This time, we don’t detect a door, so we need to invert our blue line. Once again, this allows us to filter our some particles.
In Haskell, we would write:
localizeRobot = do
-- ...
-- Drive forward a bit.
let pos2 = pos1 + 28
-- We know we're not at a door.
if not (doorAtPosition pos2)
then weight 1
else weight 0
-- ...
The next time we move, things start to get really interesting:
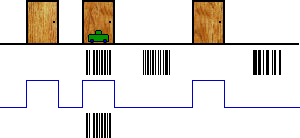
We can rule out all but one clump of particles! In Haskell:
localizeRobot = do
-- ...
-- Drive forward some more.
let pos3 = pos2 + 28
if doorAtPosition pos3
then weight 1
else weight 0
-- Our final hypothesis.
return pos3
And that’s it! We can run our particle system as follows:
> runWPS' localizeRobot 10
[97,109,93]
In this example, we run our particle system with 10 particles, 3 of which survive the whole way to the end. These are clustered about 1/3rd of the way down the hallway, giving us a pretty good idea of where we are.
Unweighted Particle System Monad
OK, so how does our monad work? This gets pretty technical, so you may want to review part 1 and part 2 before continuing. Alternatively, you could just scroll down to the last section.
To begin with, let’s ignore the weights. We can represent a particle system as function that maps an integer to a random list of particles:
newtype PS a = PS { runPS :: Int -> Rand [a] }
The integer tells us how many particles to return:
> runRand (runPS (uniform [1..10]) 5)
[3,2,9,5,10]
If we have a random value of type Rand a, we can build a
particle system of type PS a by sampling that random value
repeatedly. Building on the code from part 2, we get:
liftRand :: Rand a -> PS a
liftRand r = PS (sample r)
Given a particle system of type PS a, and a function of type
a -> b, we can construct a particle system of type PS
b by running the particle system and applying our function to each
particle:
instance Functor PS where
fmap f ps = PS mapped
where mapped n =
liftM (map f) (runPS ps n)
We also need to define the monadic return and >>=
operators. The former can be built from return operator for
Rand:
instance Monad PS where
return = liftRand . return
ps >>= f = joinPS (fmap f ps)
As for the latter, it’s usually easiest to define >>=
in terms of a join operation. And join is where
the magic happens—we need to collapse a value of type PS (PS
a) into a value of type PS a:
joinPS :: PS (PS a) -> PS a
joinPS psps = PS (joinPS' psps)
joinPS' :: PS (PS a) -> Int -> Rand [a]
joinPS' psps n = do
pss <- (runPS psps n)
xs <- sequence (map sample1 pss)
return (concat xs)
where sample1 ps = runPS ps 1
The code is a little tricky, but the basic idea is simple: We run
our outer particle system, producing n particles. But each of
these particles is itself a particle system, which we run to produce
a single particle. We then combine the n single-particle
results into one result with n particles.
We also need to make our particle system a probability monad.
Again, we can do this by reusing code from Rand:
instance Dist PS where
weighted = liftRand . weighted
Note that this monad isn’t ready for production use—it’s still pretty slow, and it doesn’t give us any way to access our sensors.
Weighted Particle System Monad
The weighted version of the particle system is a bit easier. We can just
reuse PerhapsT, which transforms an existing monad
into one with a per-element weight:
type WPS = PerhapsT PS
We also need to make WPS into a probability distribution:
instance Dist (PerhapsT PS) where
weighted = PerhapsT . weighted . map liftWeighted
where liftWeighted (x,w) = (Perhaps x 1,w)
Next, we need a way to update the weight of a given particle. Note that
this is closely related to applyProb from part 4.
weight :: Prob -> WPS ()
weight p = PerhapsT (return (Perhaps () p))
Finally, we need a way run a weighted particle system:
runWPS wps n = runPS (runPerhapsT wps) n
In our example, we also use a wrapper function to clean up the output a bit:
runWPS' wps n =
(runRand . liftM catPossible) (runWPS wps n)
catPossible (ph:phs) | impossible ph =
catPossible phs
catPossible (Perhaps x p:phs) =
x:(catPossible phs)
catPossible [] = []
You can download the latest version of this code using Darcs:
darcs get http://www.randomhacks.net/darcs/probability
In a more sophisticated implementation, we’d want to periodically resample our particles, discarding the ones with weights near zero, and increasing the number of particles near likely locations.
More cool stuff
Bayesian Filters for Location Estimation (PDF) is an excellent (and very accessible) overview of belief functions. If you’re into robotics or probability, it’s definitely worth checking out.
As sigfpe points out, PerhapsT is closely related
m-sets, which turn up a lot whenever you’re working with matrices. In
fact, you can build a monad from any measure space, including
possibility and other models of beliefs.
Don’t miss sigfpe’s excellent articles on quantum mechanics. He shows how to generalize the probability monad to support quantum amplitudes and mixed states.
Given all this cool stuff, I strongly suspect that monads are the Right Way to represent probability and beliefs in programming languages.
Want to contact me about this article? Or if you're looking for something else to read, here's a list of popular posts.
fmap. One especially cool thing about particle systems is that you can use a GPU to simulate a million particles in real-time. Given the handy monadic structure of particle systems—and their ability to represent non-linear functions--it's worth keeping particle systems in mind. With the right hardware, they're fast, flexible and easy to program.mzeroto a probability monad has tricky semantics. In the particle system above, I keep the "impossible" particles and give them a weight of 0. In a real implementation, you would generally want to replace these particles by "spliting" high-probability particles in half, or by resampling the particles periodically, resetting all the weights to 1. In an earlier hack I used the "missing probability" to represent the normalization factor needed by Bayes' rule. It's important to understand exactly howguardfits into your larger semantics; there are quite a few traps for the unwary. At a minimum, if you're going to build a sampling-based probability monad with anmzero, you're going to have to make sure thatsample 200 (guard False)immediately returns zero samples.